When a global stock market sell-off is taking place, it’s important to remain calm, but opportunistic. 

For some traders the market will move too fast for them. If you are one of those traders who struggles in a fast market, then instead of trying to fight it, take this time to work on improving your game, and focus on the fundamentals. 

This is especially true if you’re just getting into options trading… 

Over 90% of traders who jump into the world of options lose money immediately.

It’s not because they don’t have the right strategy, but mostly because they don’t know the risks that are impacting options on a daily basis.

Trading options closely related to walking in a minefield.  

One day the stock moves too much and hurts your positions or you wake up to a collapse in implied volatility that seems to come out of nowhere.  

If you are an options trader, you should have heard about “Greeks” but maybe you don’t know what exactly they are or what they can do for you.

So let’s dig into the Greeks a little further and see how each of these can help you improve your trading.

 

What can option Greeks do for you?

 

Geared up with Greeks, an options trader can make more informed decisions about the options that are available to trade.  

Here are just a few things that Greeks may help you do:

• Delta: Determine the likelihood that an option you’re considering will expire in the money.
• Gamma: Determine how much the Delta will change when the stock price changes.
• Theta: Understand how much value is lost each day as expiration approaches.
• Vega: Understand the sensitivity of an option to an increase or decrease in volatility.
• Rho: Gives the trader an estimation on the effect of interest rate changes on options. 

 

What are the Greeks?

 

Greeks, as listed above, measure different factors that impact the price of an options contract.  

Each Greek is responsible for calculating their own specific risk factors that are derived from using a theoretical options pricing model, such as, Black-Scholes.  

Since there are many market factors that impact the price of an option, we can use these models to calculate the Greeks. Then, this value gives the trader an overview of exactly how they will impact the options price when the value is changed.

For example, if we know an option moves less than the underlying stock, we can use Delta to determine how much it is expected to move when the stock moves $1.

Or, since we know that options lose value over time, a trader can reference Theta to approximate how much value is lost every day.

Now, let’s define each in further detail…

 

Delta

 

Delta is a measure of how much an option’s price is expected to change per every $1 change in the price of the underlying security. 

For example, a Delta of 0.60 means that the options price is expected to move $0.60 for every $1.00 move in the price of the underlying stock.

Let’s take a look at some specific details of each the Call and Puts.

Call Options

• Deltas range from 0.0 to 1.00
• ATM options have a Delta near 0.50
• The further options are deep in the money, the closer they get to 1.00
• Deltas of ITM call options get closer to 1.00 as expiration approaches
• Deltas of OTM call options get closer to 0.00 as expiration approaches

Put Options

• Deltas range from 0.0 to -1.00
• ATM options have a Delta near -0.50
• The further options are deep in the money, the closer they get to -1.00
• Deltas of ITM call options get closer to -1.0 as expiration approaches
• Deltas of OTM call options get closer to 0.00 as expiration approaches

So, you can think of Delta as the probability of that given opto will expire in the money.

For example, an option with a Delta of 0.60 means that the option has about a 60% chance of being in the money at expiration.

Now… this doesn’t mean your trade will or will not be profitable. That only depends on the price at which you bought or sold the options.

 

Gamma

 

The options greek, Gamma, measures the rate of change in an option’s Delta per $1 change in the price of the underlying stock. 

Since this measures the rate of change of Delta, this is considered a Second Order Greek.

The easiest way to understand Gamma is to think about it as acceleration you learned in your physics class.  

Let’s walk through Delta vs Gamma together…

Delta is only accurate at a specific price and specific time.  

The problem…In the Delta example above, once the stock moved $1, the option moved $0.60 and the Delta is no longer 0.60.  

As we stated, this $1 move would cause a call option to be deeper in the money, and would push the Delta closer to 1.00.

Now… let’s assume Delta is 0.70, up from 0.60.  The difference is 0.10, and that is Gamma.

Since Delta can never exceed 1.00, the higher Delta gets, the more Gamma decreases.

 

Theta

 

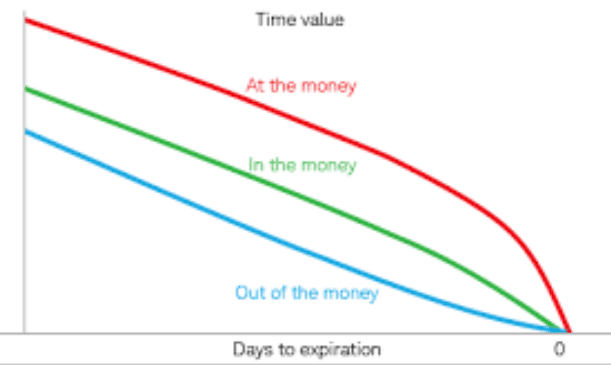
Theta is the measurement of the change in the price of an option for a 1 day decrease in its time to expiration.

In other words, Theta tells you how much the price of an option should decrease each day until it expires.  

When looking at Theta it’s decay is not linear, and as each day passes Theta increases.  

Because time decay is not linear, the Theta of ATM and ITM options generally increase as expiration approaches, and Theta of OTM options decrease as expiration approaches.

Here is a sample chart that illustrates the decay of the option over time.

 

 

Vega

 

Vega is also known as the sensitivity to volatility.

Vega measures the rate of change in an option’s price for a 1% change in the implied volatility of the underlying stock. This greek is intended to tell you how much an option’s price should move when the volatility of the underlying security increases or decreases.  

Here are some more key facts about Vega:

• Vega Measures how the implied volatility of a stock impacts the price of an option
• Volatility is one of the most important factors impacting the value of options
• When Vega drops, both the calls and the puts will lose value
• When Vega increases, both the calls and the puts will gain value

Here is a sample chart of Vega of a Butterfly spread at various levels of Implied Volatility.

 

 

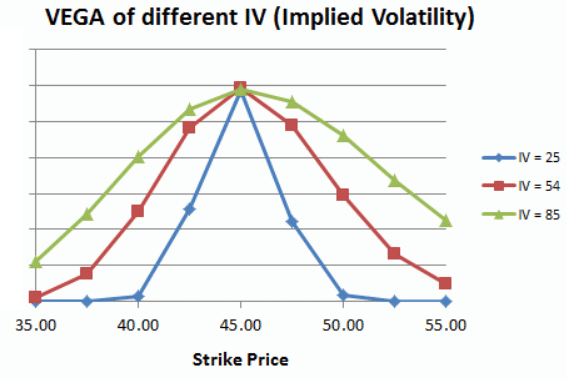
As you can tell, the higher IV becomes, the more expensive the options are at different strike price.  

Here is another view of Implied Volatility of a long put option.

 

 

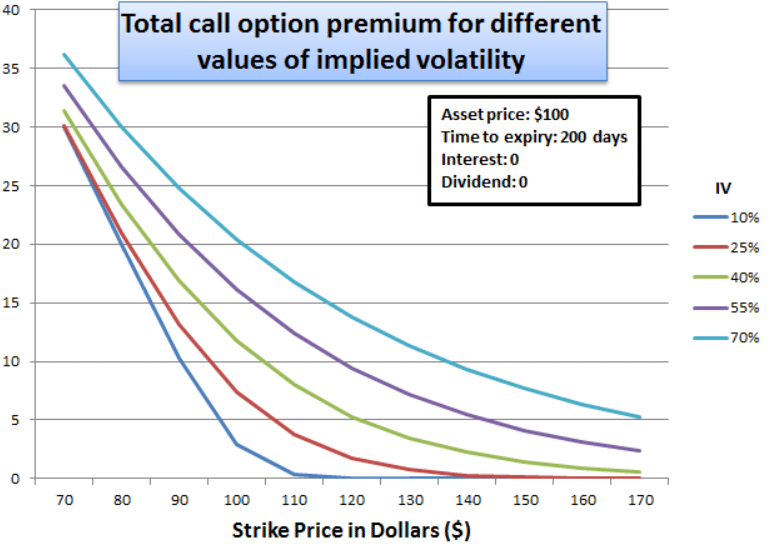
As you can see, with the increase in implied volatility impacts the stock price dramatically.

So, neglecting Vega can cause you to overpay when buying options, but when you are selling options this is a favorable boost in profits.

With all other factors being equal, when determining strategy in trading options, it’s best to consider selling options when Vega is above “normal” levels.  

One way to determine this is to compare the historical volatility to the implied volatility values.

Key points to remember:

• Implied volatility is derived from a theoretical pricing model
• Higher than normal implied volatility is more favorable for option sellers
• Lower than normal implied volatility is more favorable for option buyers
• Implied volatility is a mean reverting instrument
• Implied volatility is not consistent for all options and will be lowest for ATM options.

Rho

 

Rho measures the expected change in an option’s price per 1% point change in interest rates. It tells you how much the price of an option should raise or fall in the risk-free interest rate, such as T-Bills.  

General information about Rho:

• As interest rates increase, the value of call options will increase
• As increase rates increase, the vale of put options will decrease
• Call options have positive Rho, and put options have negative Rho.

Rho is generally not a huge factor in the price of short-term options. But when trading LEAPS, Rho can have a far greater impact on the price of these options.

 

Wrapping up

 

It’s always difficult to not only predict the movement of the stock market but also take into consideration all the various aspects of option prices as well.

And that’s why trading the cornerstone strategy for Options Profit Planner takes away the headaches of dealing with all of these various factors.  

This strategy focuses on finding key stocks that typically have an increased volatility.  

By selling put spreads, OPP aims to take advantage of not only implied volatility, or vega, but also the direction of the underlying stock may move.  

If you want to learn more about my approach to trading then check out this recent training workshop I put together. Click here to watch it now.